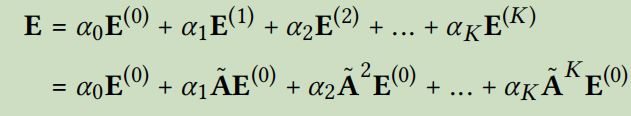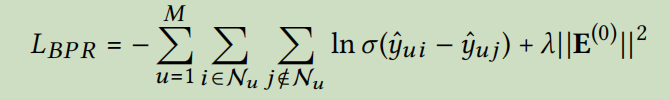LightGCN阅读笔记

​ 现有的将GCN缺乏对GCN的消融分析，并且该论文发现特征变换和非线性激活对协同过滤一点用都没有，甚至增加了训练的难度并且降低了推荐的效果。

​ 造成上面结果的原因是，GCN最初是应用于属性图上的节点分类，其中每个节点都有丰富的属性作为属性特征，而在协同过滤的用户-项目交互图中，每个节点只有一个独热编码的ID来描述，这个ID只能作为标识符，没有具体的语义。所以如果再执行多层非线性转换不仅不会带来任何好处，反而会增加模型训练的难度。

LightGCN模型结构

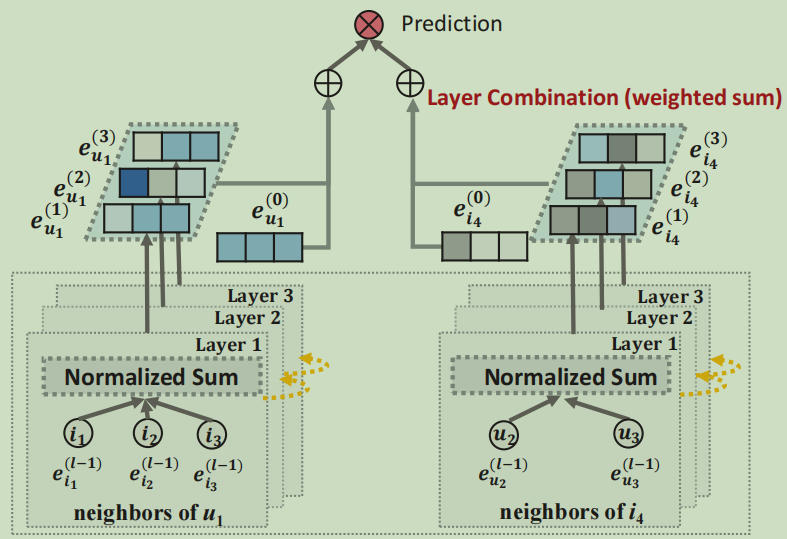
​ LightGCN的模型结构：

​

​ LightGCN只包含GCN中最基本的组件，很大的简化了模型的设计，在LightGCN中，我们只采用简单的加权和聚合，不再使用特征变换和非线性激活

​ 信息传递和聚合的规则为：

​ $$ e_u^{k+1}=\sum_{i\in N_u}\frac{1}{\sqrt{

N_u

}\sqrt{

N_i

}}e_i^k $$

​ $$ e_i^{k+1}=\sum_{i\in N_i}\frac{1}{\sqrt{

N_u

}\sqrt{

N_i

}}e_u^k $$

在聚合的过程中，我们只聚合连接的邻居，而不聚合自己

在LightGCN中，唯一可以训练的参数是初始的embedding

在经过K层LGC后，我们可以进一步结合在每一层获得的embedding，形成最终的表示。

多层嵌入的结合规则为：

$e_u=\sum_{k=0}^K\alpha_ke_u^k;e_i=\sum_{k=0}^K\alpha_ke_i^k$

K为层数，$\alpha_k$表示第k层的权重，可以手动指定也可以作为训练参数

​ 结合在每一层的原因主要有三点

• 随着层数的增加，会出现过度平滑的问题，因此不能简单的使用最后一层
• 在不同层的嵌入捕捉到了不同的语义，所以结合起来将会更加全面
• 将不同层的embedding使用不同的加权结合起来，可以获得自链接的效果

最终模型的预测定义为用户和项目最终表示的内积

$\hat{y}_{ui}=e_u^Te_i$

这个就被作为推荐生成的排名分数

LightGCN的矩阵表示

用户和物品的邻接矩阵表示为

\[A=\begin{pmatrix} 0&R \\ R^T&0 \end{pmatrix}\]

R表示了用户与物品的关系，如果用户u和物品i有联系，则$R_{ui}=1$，否则为0

LGC的矩阵表示为

$E^{k+1}=(D^{-\frac{1}{2}}AD^{-\frac{1}{2}})E^k$

其中矩阵D为度矩阵，$D_{ii}$表示了第i个对象的度

之所以使用$D^{-\frac{1}{2}}$是为了降低高度数的节点的影响，邻居节点的度数越高，对本节点的影响就越小

最终的embedding矩阵为：

其中$\tilde{A}=D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$

模型训练

该模型的损失函数为BPR损失函数

下载链接为：https://www.dropbox.com/scl/fi/2uxzxljq0jigbvouup6pp/LightGCN.pdf?rlkey=opi07e8mgdo84r9h2iyhpdvok&dl=0